This is a part-post from Developing Project Schedule project management activity post. You will learn how to calculate critical path, float/slack, early & late starts, and early & late finishes of a network path in this article.
For easier understanding this post is divided into four parts that can be navigable at the bottom of each part.
I suggest you get yourself a cup of your favorite beverage (I was going to say Coffee), this one is going to be a long ride. 🙂
As we saw in Developing Project Schedule project management activity, Critical path is made up of series of activities from beginning to the end, where each activity has a dependency over previous activity in such a way that delay in any one activity causes delay in all subsequent activities, causing the project to slip.
In other words, critical path is the longest path in your project’s schedule network diagram, and is the SHORTEST possible duration for the project.
How to Calculate Critical Path
Let us take a simpler example than John’s home construction example we saw in previous lessons.
This project involves assembling a train set.
Calculating Critical Path is a simple 4-step process.
Step 1: Find Activities
Activities for this project are as below (output from Define Activities process) –
- Assemble two-tier bridge
- Join winding tracks
- Assemble and add train station
- Place standalone items around
- Assemble and add construction site
- Join train engine and bogies
- Place the train on the track
- Start the engine and let it chug!
Step 2: Build Schedule Network Diagram
Sequence activities and build schedule network diagram (output from Sequence Activities process) . This is how it looks, with individual activity duration in minutes –
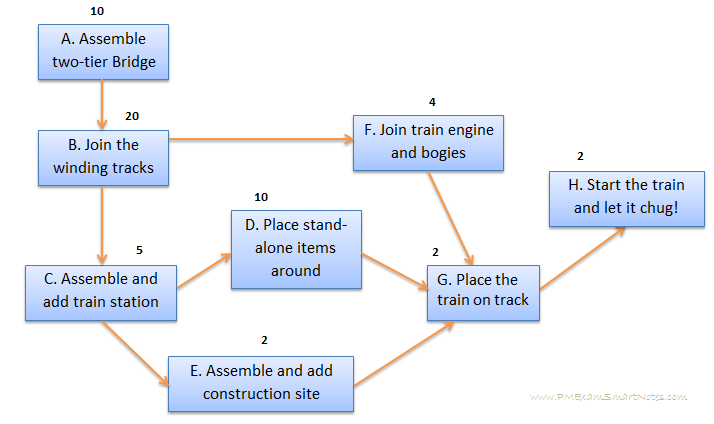Figure 2: Assemble train set – schedule network diagram
Step 3: Find all Possible Paths
Find all possible paths through the diagram, there are 3 in our case –
A -> B -> F -> G -> H
A -> B -> C -> D -> G -> H
A -> B -> C -> E -> G -> H
Step 4: Calculate Duration for Each Path
Let us see the duration for each of these paths –
A -> B -> F -> G -> H —> 10+20+4+2+2 = 38 minutes
A -> B -> C -> D -> G -> H —> 10+20+5+10+2+2 = 49 minutes
A -> B -> C -> E -> G -> H —> 10+20+5+2+2+2= 41 minutes
The network path with longest total duration is the critical path!
Critical path is the shortest duration required to complete the project successfully.
In our example this is the second path:Â A -> B -> C -> D -> G -> H, which comes to 49 minutes.
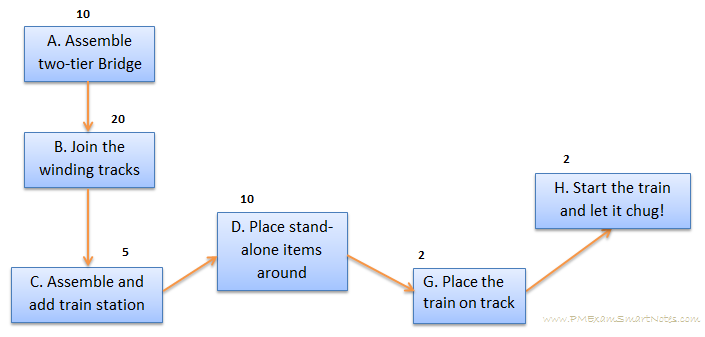Figure 3: Assemble train set – Critical Path
Note that sum of durations of all activities on critical path comes 49 minutes, and sum of duration of ALL activities on the project is much longer. If managed well, the whole project can be completed within the critical path’s duration.
In the next page, let us see how to calculate Float for activities..
(please use the page numbered link below to navigate)..
